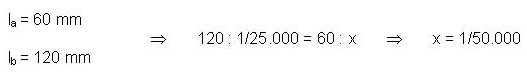La cartografia si occupa della rappresentazione grafica della superficie fisica della terra o di sue porzioni e dei metodi matematici che consentono tale rappresentazione. I metodi matematici consistono sostanzialmente nel trovare due funzioni che consentano di passare da un punto posizionato sulla superficie terrestre al corrispondente punto sulla carta. Per ogni proiezione esiste, cioè, un sistema di formule matematiche del tipo
che fanno corrispondere l’ascissa x e l’ordinata y del punto immagine alle sue coordinate geografiche (latitudine e longitudine ) La posizione dei punti della superficie terrestre viene determinata in relazione ad un sistema di riferimento (o datum) sul quale viene definito un opportuno sistema di coordinate. Il sistema di riferimento tradizionalmente rappresenta una superficie che, localmente, approssima in maniera opportuna la superficie terrestre. La superficie terrestre è rappresentato da due superfici "di base" - l’ellissoide
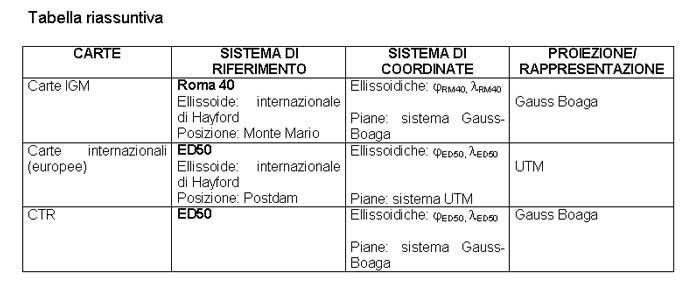
La cartografia regionale è riferita al sistema ED50.
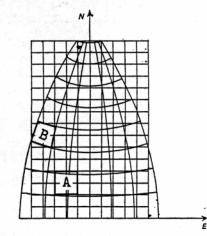
Le coordinate geografiche sono coordinate ellissoidiche, perciò “sferiche” perché designano la posizione dei punti su una superficie ellissoidica (o sferica). I meridiani ed i paralleli sul globo non sono linee rette equidistanti né formano un reticolo di questo tipo su alcuna delle proiezioni cartografiche di largo uso. E’ perciò opportuno introdurre un sistema di coordinate completamente diverso al fine di poter usufruire nelle carte di un reticolato ortogonale ed equidistante: il sistema di coordinate piane. Questo reticolato, costituito da quadrati sulla carta, viene sovrapposto al reticolato geografico. Il sistema di coordinate piane oggi maggiormente utilizzato è il reticolato chilometrico che si riferisce alla proiezione universale trasversa di Mercatore (UTM). Il reticolato italiano si riferisce alla proiezione di Gauss-Boaga, ellissoide internazionale, anche se in molte carte topografiche italiane alla scala [2] 1:25.000 sono indicati entrambi i tipi di reticolato (UTM e Gauss-Boaga). Utilizzando il reticolato chilometrico le coordinate del punto “x” ed “y” vengono fornite in metri.
Il geoide rappresenta la superficie che meglio approssima la forma della terra poiché tiene conto dell’azione combinata della rotazione terrestre attorno al proprio asse e della distribuzione disomogenea delle masse. A causa di questi due fattori, la superficie terrestre assume una forma più complessa di un ellissoide, la quale è in ogni punto ben definita e individuabile (poiché è caratterizzata da una direzione caratteristica, la direzione della verticale, ovvero la direzione secondo la quale si dispone un filo a piombo sospeso per l’altra estremità); si tratta di una superficie fisicamente riproducibile, ma non trattabile matematicamente. Poiché la quota di un punto risente dell’attrazione delle masse e quindi di esse deve tenere conto, il geoide rappresenta la superficie di riferimento per quanto riguarda l’aspetto altimetrico (coordinata “z”). Il geoide, non essendo una superficie trattabile matematicamente, viene definito per punti ed assume perciò, anche in questo caso, un significato “locale”. La definizione della superficie geoidica prevede che essa, partendo da un punto del livello medio del mare (definito statisticamente in vari punti), si mantenga costantemente normale ad un sistema di linee verticali condotte per i punti della superficie fisica terrestre. In un punto generico, la verticale viene determinata con l’ausilio di un filo a piombo; nel momento in cui si fa stazione con uno strumento in un punto, l’asse dello strumento viene messo in verticale proprio rispetto al geoide. Il sistema altimetrico ha dei riferimenti: il geoide è identificato da uno zero posto a Genova ed è realizzato mediante la rete di livellazione di alta precisione. Le quote riportate sulle carte derivano, quindi, da Genova, ad eccezione di quelle della Sicilia e della Sardegna (in quanto la livellazione si ferma davanti ad un ostacolo, rappresentato in questo caso dal mare). Per l’altimetria, perciò, non esistono tutti i sistemi di riferimento come per la componente planimetrica ma solo tre [3] .
Stabilita la posizione di un punto della superficie terrestre secondo
i criteri sopra enunciati, la rappresentazione grafica di tale punto
consiste, in sostanza, nella sua proiezione sul piano. Nella cartografia
ufficiale tale operazione viene effettuata considerando la forma ellissoidica
della terra, tuttavia, in una trattazione elementare e descrittiva delle
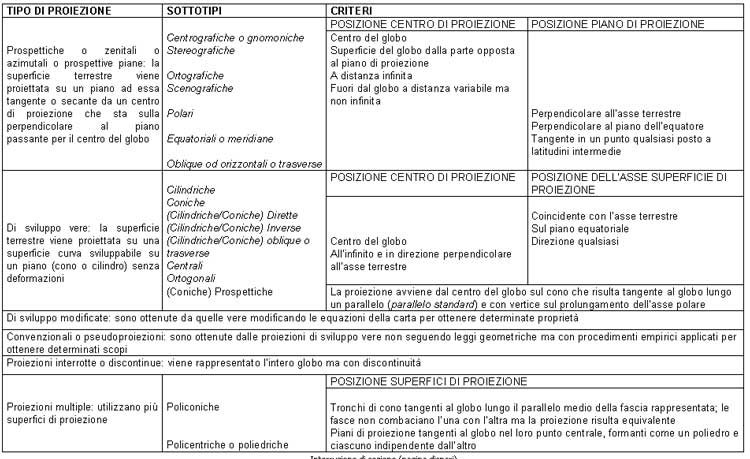
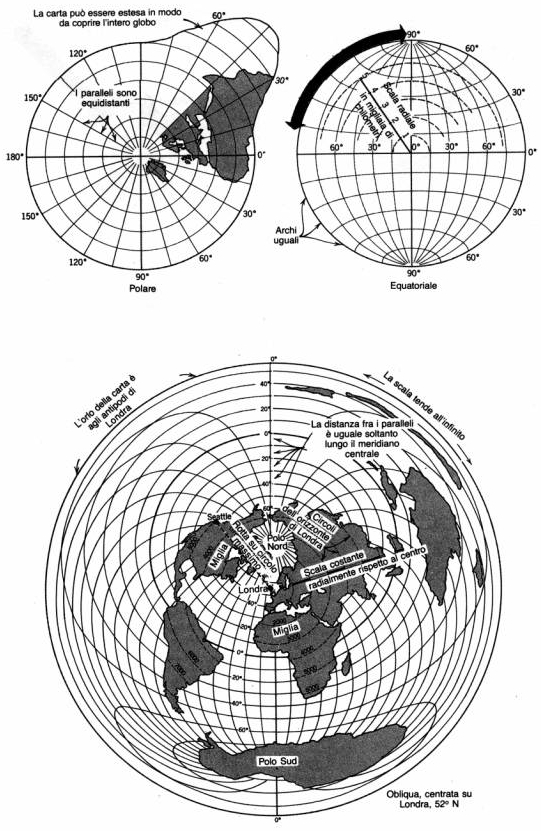
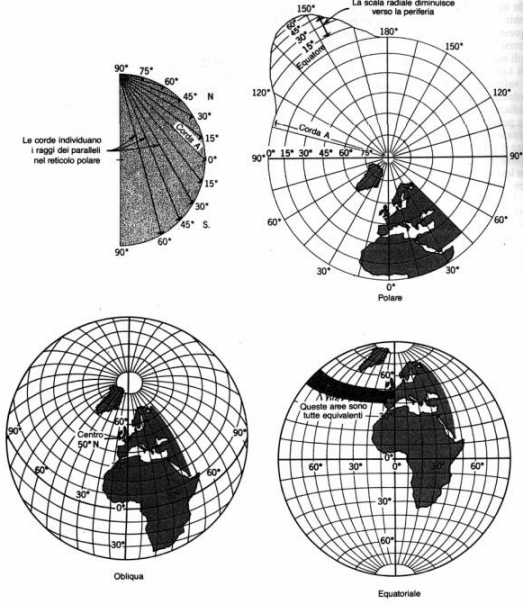
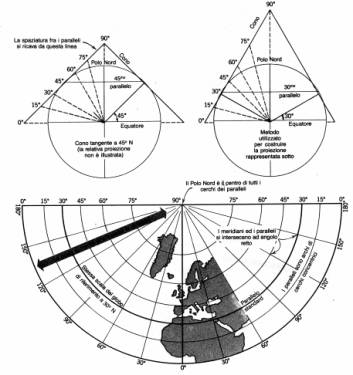
proiezioni, la terra può venire considerata come una vera sfera. · carte conformi (o ortomorfiche): ogni piccola porzione della superficie terrestre conserva sulla carta la stessa forma che possiede sul globo. Nelle carte conformi i meridiani ed i paralleli si intersecano ovunque secondo angoli retti (come su un globo), ma non tutte le proiezioni dove ciò accade sono conformi.
Le carte conformi sono isogoniche ma non tutte le carte isogoniche sono conformi.
[4] Su un globo si conservano
proprietà di equidistanza in tutte le direzioni
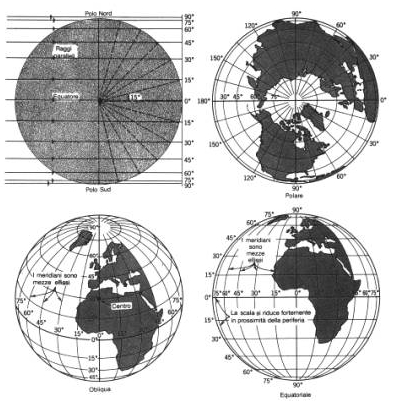
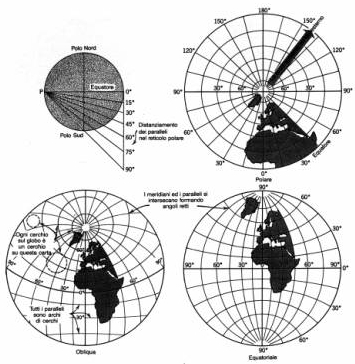
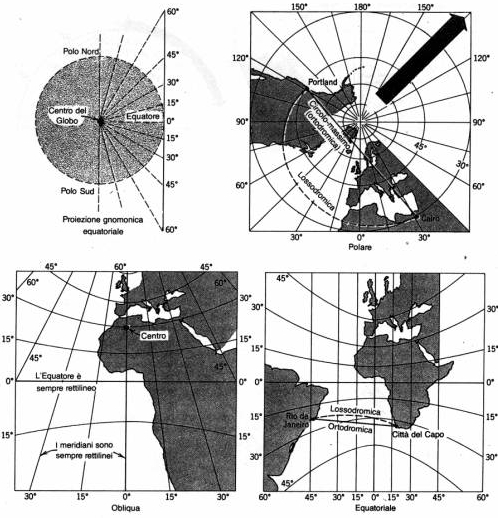
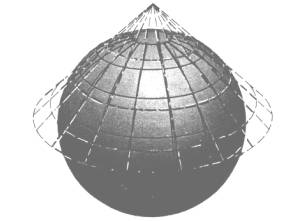
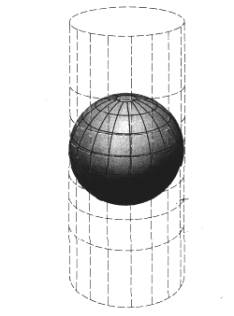
Dal punto di vista geometrico, i metodi di rappresentazione sono raggruppabili secondo la tabella riportata nel seguito.
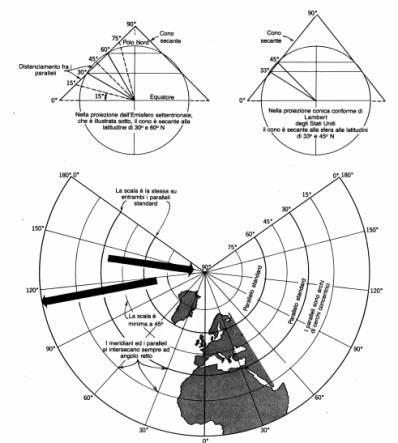
Un esempio importante di proiezione equivalente è quella di Cassini-Soldner utilizzata dal Catasto Italiano per la redazione delle mappe catastali.
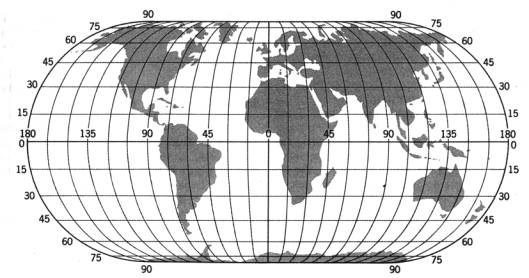
Proiezione equivalente di Lambert. E’ una proiezione cilindrica diretta ortogonale in cui il centro di proiezione è all’infinito ma mobile e sempre sul piano del meridiano proiettato. I paralleli ed i meridiani sono rettilinei e perpendicolari tra loro, formando maglie rettangolari, ma i paralleli si avvicinano tra loro verso i poli, per cui le regioni polari sono schiacciate.
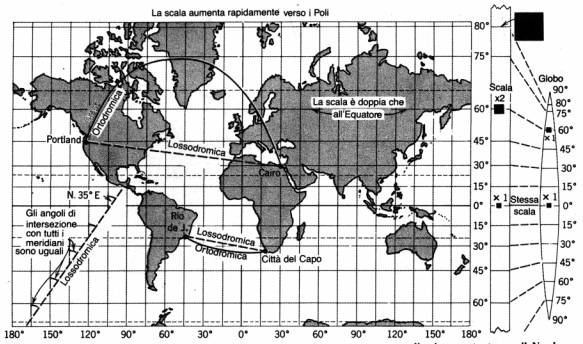
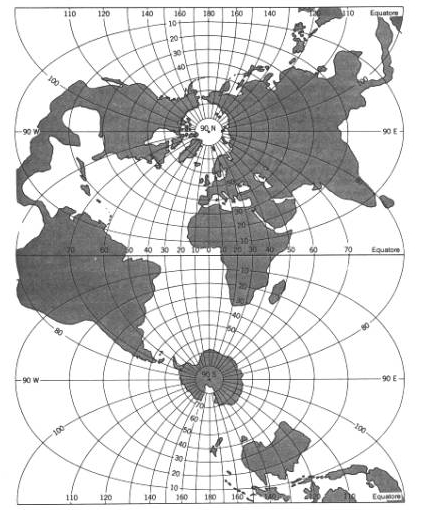
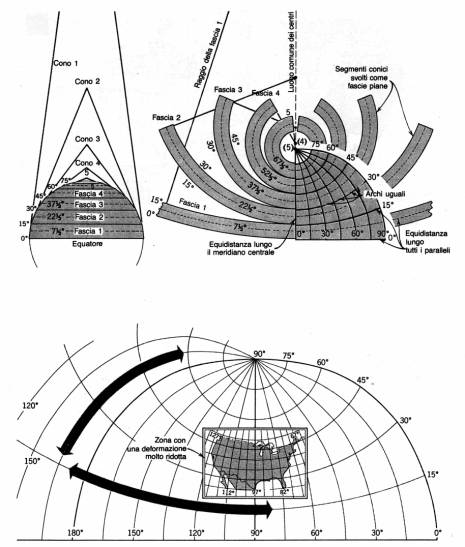
Proiezione di Mercatore. Si tratta di una proiezione cilindrica modificata nella quale le equazioni della carta sono state stabilite in modo da ottenere l’isogonicità. I meridiani sono linee verticali diritte ed equidistanti, i paralleli sono linee diritte perpendicolari ai meridiani e tutte della stessa lunghezza. Perciò la scala del globo di riferimento viene rispettata soltanto lungo l’equatore, mentre aumenta lungo i paralleli con il crescere della latitudine per tendere all’infinito verso i poli, che diventano linee lunghe come l’equatore. La proiezione classica di Mercatore è di tipo equatoriale, cioè il cilindro è tangente all’equatore ed il suo asse coincide con l’asse terrestre . [5]
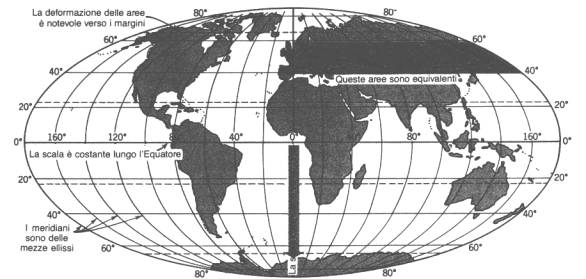
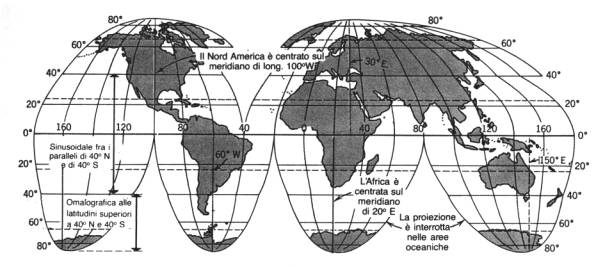
Proiezione omalografica di Mollweide o di Babinet. Si tratta di una proiezione pseudocilindrica in cui un emisfero è delimitato da un cerchio, mentre l’altro risulta suddiviso in due parti con un contorno ellittico, aggiunte sui due lati del cerchio. La carta costruita con tale proiezione è una carta equivalente adatta soprattutto a rappresentare la distribuzione areale delle zone geografiche e politiche del globo. Tuttavia presenta forti distorsioni per le regioni polari
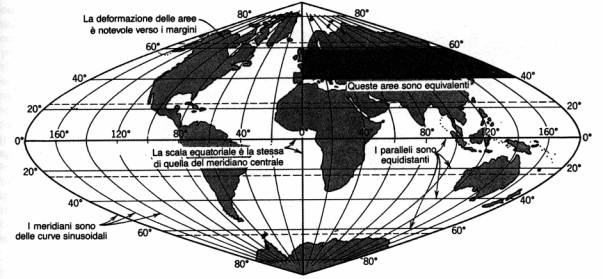
Proiezione sinusoidale di Sanson-Flamsteed. E’ una proiezione pseudocilindrica equivalente con un meridiano diritto centrale e con paralleli orizzontali e diritti. I meridiani sono costituiti da famiglie di curve sinusoidali.
Proiezione omalosina (di Goode). Si tratta di una combinazione della proiezione omalografica e sinusoidale. E’ un tipo di proiezione adatto per carte mondiali relative a fenomeni areali.
Proiezione universale trasversa di Mercatore (UTM) o conforme di Gauss. E’ una proiezione pseudocilindrica assimilabile alla cilindrica inversa, ma le sue equazioni della carta sono state costruite in modo da ottenere l’isogonicità. In essa sono rettilinei e tra loro perpendicolari solo il meridiano di contatto con il cilindro e l’equatore. Gli altri meridiani e paralleli sono curve complesse che soddisfano le equazioni della carta.
Proiezione di Bonne. Si tratta di una rappresentazione pseudoconica equivalente ottenuta con un cono tangente; i paralleli sono archi di cerchio con lunghezza proporzionale a quella vera e i meridiani sono curve ottenute facendoli passare per punti tra cui esista, lungo ciascun parallelo, una distanza proporzionale a quella vera. Con questa proiezione fu costruita la carta d’Italia del 1889, in 35 fogli, alla scala a1:500.000 e la carta di Francia del 1878 a scala 1:80.000. Proiezione IV di Eckert. E’ una proeizione sinusoidale equivalente con i paralleli orizzontali, molto usata in Europa. I meridiani sono delle ellissi spaziate in maniera equidistante su ciascun parallelo. Come la proiezione omalosina, quella di Eckert è un tipo di proiezione adatto per carte mondiali relative a fenomeni areali.
Proiezione policentrica o poliedrica. Si hanno tanti piani di proiezione tangenti al globo nel loro punto centrale, formanti come un poliedro, e ciascuno indipendente dall’altro. Su questo tipo di proiezione è basata la costruzione dei fogli alla scala 1:100.000 della carta d’Italia che fu completata nel 1900 (cfr. paragrafo successivo).
Si riporta una tabella che presenta alcuni criteri di classificazione delle carte.
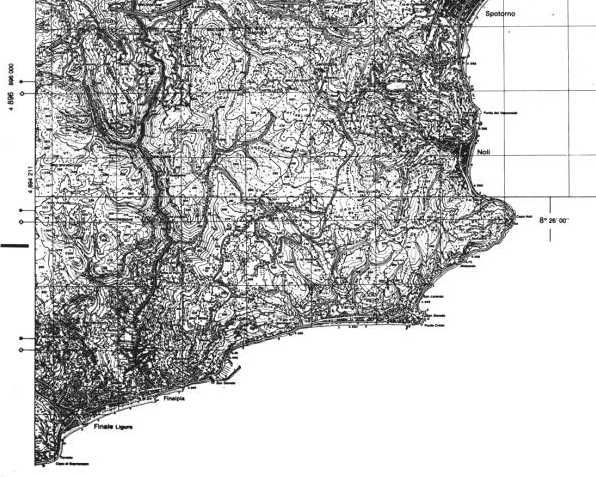
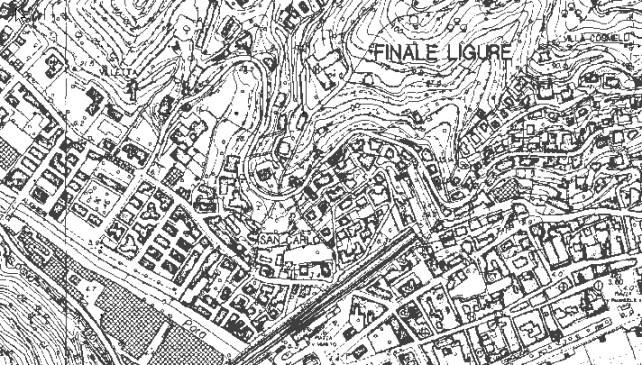
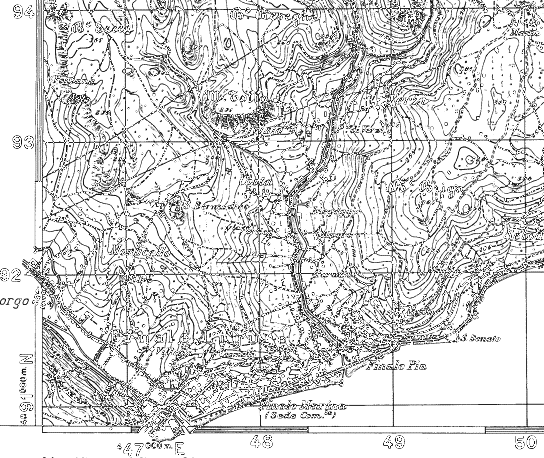
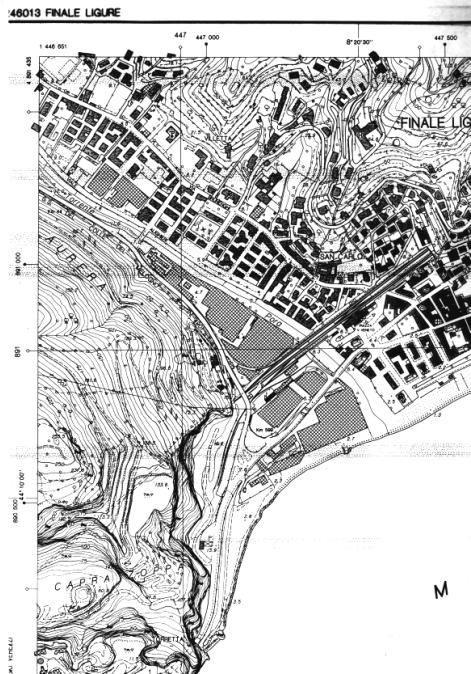
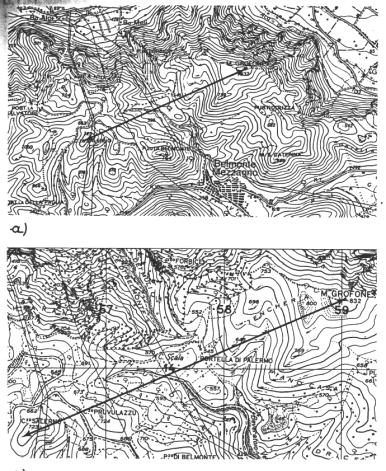
Il concetto di scala è fondamentale sia dal punto di vista operativo sia per quanto riguarda la corretta interpretazione e restituzione delle informazioni. Si definisce scala il rapporto numerico tra le misure lineari rappresentate sulla carta e quelle reali corrispondenti. Le informazioni riportate sulla cartografia, sia essa di base o derivata, sono in funzione della scala di rappresentazione del dato e del grado di precisione della rappresentazione: minore è la scala minore è il dettaglio della rappresentazione. Di grande importanza risulta la considerazione della scala di acquisizione del dato, cioè del grado di dettaglio “iniziale” a cui è stato rilevato il dato: la scala catografica non può essere inferiore alla scala di acquisizione; cioè è scorretto, in generale, ingrandire una cartografia per ottenere una scala minore, indipendentemente dal tipo di cartografia utilizzata. A titolo di esempio nelle figure seguenti vengono riportate alcune immagini relative a scale diverse della stessa zona per evidenziare il diverso tipo di informazioni in esse contenute.
Nei paragrafi seguenti si farà riferimento ad indicazioni ed operazioni riferite alla cartografia di base perché questa rappresenta il riferimento comune agli altri tipi di cartografia, con particolare riferimento alla cartografia tematica. La conoscenza e la corretta interpretazione delle informazioni contenute nelle carte di base rappresenta quindi un elemento fondamentale per passare poi all’utilizzo ed alla interpretazione dei tematismi, i quali cosituiscono un indispensabile strumento progettuale e di lettura del territorio.
Detta carta è costituita dai seguenti elementi.
Come precedentemente accennato, la cartografia ufficiale italiana è basata sulla proiezione di Samson-Flamsteed, che nasce dall’inviluppo dell’ellissoide in un poliedro (ogni Foglio al 100.000 coincide con una faccia del poliedro) per cui ognuno di questi fogli risulta tangente all’ellissoide nel suo punto centrale. Tale proiezione venne introdotta in sostituzione di altre rappresentazioni non omogenee (Bonne, Cassini) con le quali erano state redatte le carte dei diversi Stati riuniti poi nel Regno d’Italia. Ciascun foglio costruito in questo modo ha la forma di un trapezio isoscele mistilineo con basi rettilinee e lati curvi ad andamento sinusoidale riferiti ad assi passanti per il centro. Tale proiezione policentrica presenta il vantaggio che gli errori, limitati alla zona marginale, sono piccolissimi, per cui la carta si può considerare equivalente e conforme, in pratica, anche se non lo è rigorosamente. Essa però ha l’inconveniente che due fogli adiacenti non combaciano, per cui è difficile, ad esempio, determinare la distanza tra due punti appartenenti a fogli diversi. Per ovviare a tale inconveniente nel costruire la nuova carta d’Italia, in particolare le tavolette al 25.000, da cui si fanno derivare per riduzione i quadranti a scala 1:50.000 ed i fogli a scala 1:100.000, nel 1940 fu scelta, dall’Istituto Geografico Militare, sotto la direzione di G. Boaga, la proiezione conforme di Gauss, con cilindro secante, nota come rappresentazione di Gauss-Boaga. Per limitare le deformazioni è stato stabilito di suddividere il territorio italiano in due fusi di 6° di ampiezza ciascuno, potendo in tal modo garantire la precisione necessaria anche nei calcoli geodetici. Il fuso ovest è compreso fra il meridiano di Monte Mario e quello di 6° E Greenwich (ossia 6°27’08” O di Monte Mario). Il fuso est è compreso fra 11°57’08” E (ossia 0°30’ O di Monte Mario) e 18°30’ E (ossia 6°02’51” E di Monte Mario). Per limitare le deformazioni è stato stabilito di suddividere il territorio italiano in due fusi di 6° di ampiezza ciascuno, potendo in tal modo garantire la precisione necessaria anche nei calcoli geodetici. Il fuso ovest è compreso fra il meridiano di Monte Mario e quello di 6° E Greenwich (ossia 6°27’08” O di Monte Mario). Il fuso est è compreso fra 11°57’08” E (ossia 0°30’ O di Monte Mario) e 18°30’ E (ossia 6°02’51” E di Monte Mario) [7] .
I meridiani di riferimento dei fusi si fanno risultare quelli di 9°E e di 15° E Greenwich per consentire il facile inserimento nel sistema UTM mondiale (cfr. oltre). Allo scopo di utilizzare il vecchio materiale cartografico, la squadratura dei fogli, anziché rispettare la suddivisione di 30’ in 30’ Greenwich, si fa iniziare dal meridiano di Monte Mario (12°27’08”.4) come nella proiezione naturale, e cioè in modo che l’ultima striscia di fogli al 100.000 del fuso ovest coincida con la prima striscia del fuso est entro la longitudine di 11°57’08”.4 e 12°27’08”.4, per un’estensione di 30’ che è appunto la larghezza di un foglio. In tale zona di sovrapposizione si è eseguita la cartografia rispetto ad entrambi i fusi. La zona di sovrapposizione è resa necessaria per risolvere i problemi relativi a punti situati nelle vicinanze del meridiano di separazione ma su fusi diversi [8] .
Le carte ora descritte sono riferite ad un sistema di coordiante che prende il nome dalla proiezione su cui si basa: il reticolato Gauss-Boaga, noto come sistema Gauss-Boaga. Il sistema Gauss-Boaga è costituito da una quadrettatura le cui maglie quadrate hanno lati rappresentati da 1 Km o suoi sottomultipli ed è riferito ad un sistema di assi cartesiani di cui uno rappresenta l’equatore e l’altro il meridiano centrale del fuso. Il
sistema Gauss-Boaga è costituito da un sistema di assi cartesiani avente
l’asse delle ascisse (X) positivo verso est, quello delle ordinate
(Y) positivo verso nord.
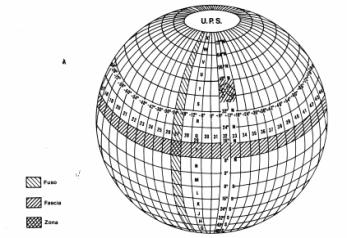
Si sono prese queste ascisse convenzionali per centri dei due fusi perché il primo numero indica il numero del fuso e perché non vi è possibilità di equivoco nell’individuare un punto a qualsiasi fuso appartenga (1° di longitudine per l’Italia ha uno sviluppo che non raggiunge i 100 Km). La ragione dell’aver scelto 2520 Km come ascissa del centro del fuso est e non ad es. 2500 sta nell’opportunità che, nella zona di sovrapposizione, uno stesso punto, nei due fusi, non possa avere lo stesso numero di decine (come sicuramente non ha quello delle centinaia e delle migliaia), a scanso di equivoci. Le coordinate di un punto rispetto agli assi cartesiani prendono il nome di: Coordinata E (est), le ascisse rispetto all’origine convenzionale, relative al valore stabilito per il meridiano centrale Coordinata N (nord), le ordinate rispetto all’equatore. Queste coordiante sono sempre positive, essendo l’Italia a nord dell’equatore ed avendo preso per il meridiano centrale (origine) un’ascissa positiva grande. Le successive fasi di aggiornamento e produzione di cartografia hanno previsto l’utilizzo di tecniche fotogrammetriche: il rilievo del terreno che si avvale di tali tecniche consiste nello sfruttamento metrico dell’immagine del territorio ripreso da coppie di foto aeree che permettono di ricreare la costruzione tridimensionale. L’IGM ha provveduto ad eseguire, a partire dal 1983, riprese a media scala per circa 45.000 Kmq/anno, sia ai fini della copertura sistematica del territorio nazionale sia per soddisfare le esigenze connesse con la cartografia. In aggiunta, a partire dal 1989 sono stati effettuati rilevamenti multispettrali ed all’infrarosso fotografico per circa 30.000 Kmq/anno. L’obiettivo è quello di fornire un insieme completo ed aggiornato di informazioni territoriali utili ai fini dello studio dei fenomeni ambientali.Anche nella cartografia internazionale prodotta utilizzando la proiezione UTM il sistema di coordinate prende il nome dalla proiezione su cui si basa essendo perciò denominato sistema UTM. Esso riguarda le latitudini comprese tra 80° sud e 80° nord [10] econsiste di 60 spicchi detti fusi ciascuno della larghezza di 6° di longitudine e di 20 fasce ciascuna dell’ampiezza di 8° di latitudine. L’aggiunta di mezzo grado su entrambi i lati fornisce una zona di sovrapposizione con i fusi adiacenti.
Per eseguire una carta relativa al territorio di molte nazioni, si è dovuto provvedere alla revisione di tutta la rete di appoggio, ossia delle triangolazioni dei vari stati, onde procedere ad una compensazione in blocco e a stabilire l’orientamento dell’ellissoide (internazionale) rispetto alla superficie di riferimento effettiva nel punto più conveniente per tutta la rete; tael punto è risultato, per l’Europa occidentale, in Germania. La cartografia italiana è redatta invece in base alla triangolazione compensata indipendentemente dalle altre e riferita all’ellissoide orientato a Monte Mario. Ciò porta come conseguenza che gli elementi cartografici, nel sistema Gauss-Boaga, non si innestano perfettamente nella rete UTM ma danno luogo a delle differenze, alcune delle quali arrivano quasi a 200 m [11] .
La Cartografia Tecnica Regionale (CTR) é rappresentata nella proiezione di Gauss, inquadrata nel sistema Geografico Europeo Unificato ED 1950, ma con coordinate piane riferite al sistema nazionale di Gauss Boaga, su fogli di carta aventi le dimensioni di 707x1.000 mmq, corrispondenti al formato B1 della classificazione UNI, secondo quanto indicato nel fascicolo "Norme proposte per la formazione di Carte Tecniche alle scale 1:5000 e 1:10000" della Commissione Geodetica Italiana. Il taglio, la cornice, il numero distintivo di ciascun foglio alla scala 1:10000 ed 1:5000 sono così definiti: ogni foglio alla scala 1:10000, denominato Sezione , è limitato dalle trasformate di due paralleli di latitudine di 3' e dalle trasformate di due meridiani aventi una differenza di longitudine di 5' e rappresenta la 16ma parte del foglio della Carta d'Italia alla scala 1:50000. Ogni sezione è contraddistinta da un nome di località seguito da un numero di sei cifre, le cui prime tre indicano il foglio alla scala 1:50000 in cui si trova, la quarta e la quinta cifra (variabile da 01 a 16) precisano la posizione che occupa sul foglio al 50000, e la sesta cifra è sempre zero. Ad esempio: ALBENGA 245150; ogni foglio alla scala 1:5000, denominato Elemento , è limitato dalle trasformate di due paralleli e di due meridiani aventi rispettivamente una differenza di latitudine di 1'30" e di longitudine di 2'30". Ciascun elemento rappresenta la quarta parte di una Sezione ed è contraddistinto da un nome di località seguito da un numero di sei cifre di cui le prime cinque sono uguali a quelle della Sezione a cui l'elemento appartiene e la sesta (variabile da 1 a 4) precisa la posizione che occupa nella Sezione: esempio: CISANO SUL NEVA 245101. I particolari del territorio di origine naturale ed artificiale riportati sulla carta tecnica,che ne costituiscono il contenuto plano-altimetrico, sono quelli elencati nel cap. 6 del fascicolo delle "Norme tecniche" della Commissione Geodetica Italiana e codificati in una apposita "Libreria" messa a punto dalla Regione Liguria. La cartografia regionale riporta indicazioni di inquadramento rispetto al resto della cartografia ufficiale (cfr. Appendice 1). Tabella riassuntiva
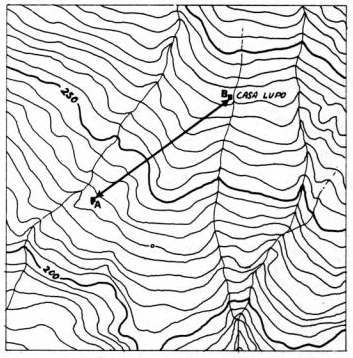
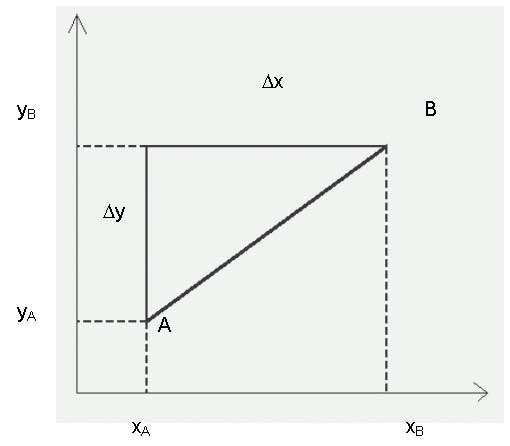
- calcolo della distanza topografica (=distanza orizzontale che prescinde dalla quota dei due punti)
2. Conoscendo le coordinate dei vertici del segmento si procede nel seguente modo
- trasporto di una distanza reale sulla carta Il valore della distanza reale dovrà essere diviso per il numeratore
della scala - determinazione della scala incognita di una carta
2) Se si effettuano misure dirette sul terreno è sufficiente
effettuare il rapporto tra le misure sulla carta e quella corrispondente
misurata sul terreno. - Informazione altimetrica · Informazione altimetrica · Orientamento con la carta
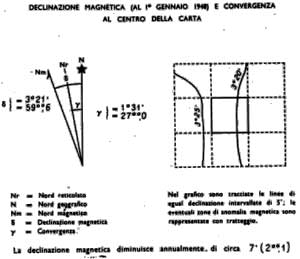
Ottenuto il valore della declinazione magnetica attuale e la posizione del Nm rispetto al N si opera sul grafico stampato alla destra della tavoletta e centrale nel foglio al 50.000: si trova nella scala graduata il valore corrispondente alla declinazione calcolata e si congiunge con il punto in basso alla estremità del grafico. La direzione materializzata rappresenta la direzione del Nm attuale. Per le operazioni di orientamento della carta con la bussola basterà far coincidere l’asse dell’ago della bussola con la direzione trovata e non con il segmento relativo al tratto di meridiano passante per il luogo.
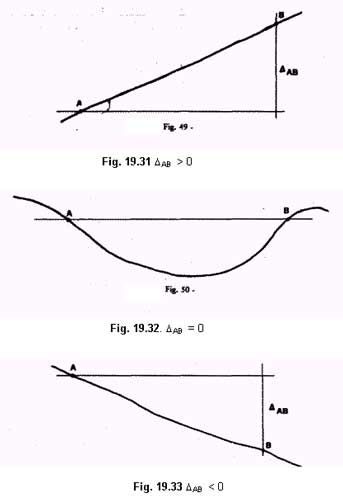
· Dislivelli
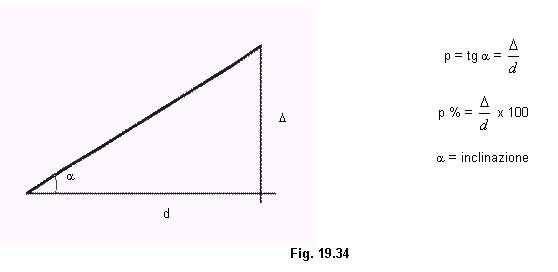
Pendenze
Ubicazione e quota di un punto Sistema UTM 1) Procedimento diretto (nota la posizione sulla carta si ricavano le coordinate)
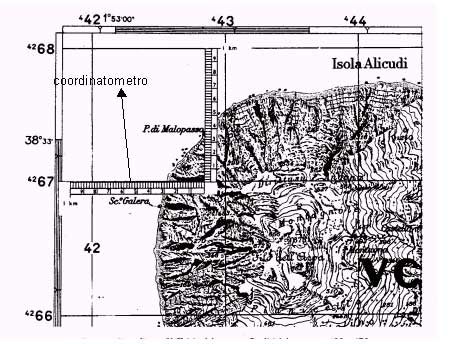
Volendo approssimare fino all’ettometro si riporta la distanza tra il punto e il meridiano/parallelo reticolato sul coordinatometro e si legge direttamente il valore.
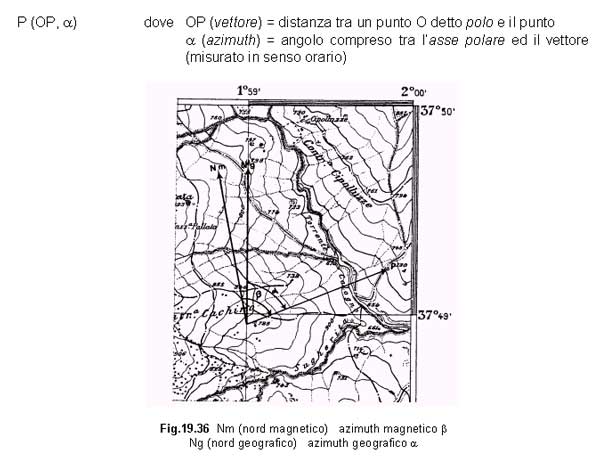
- Coordinate polari 1) Procedimento diretto
2) Procedimento inverso Nota la posizione del polo cui ci si riferisce e la direzione dell’asse polare [12], si traccia la semiretta che rappresenta l’asse polare sulla base della quale si individua l’azimuth e la lunghezza del vettore.
- Coordinate geografiche 1) Procedimento diretto
Se si fa riferimento al meridiano di Greenwich, i valori di longitudine aumentano verso est (cioè a destra della carta). Se si fa riferimento al meridiano di Monte Mario avremo due casi:a) punti con longitudine est (i valori di longitudine aumentano verso destra) b) punti con longitudine ovest (i valori di longitudine aumentano verso sinistra)
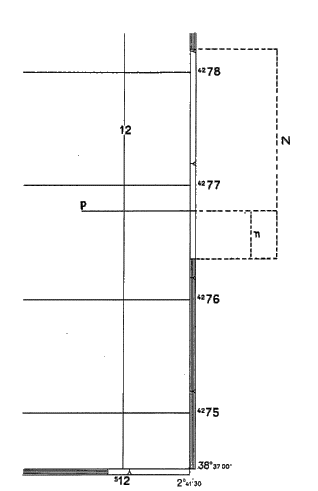
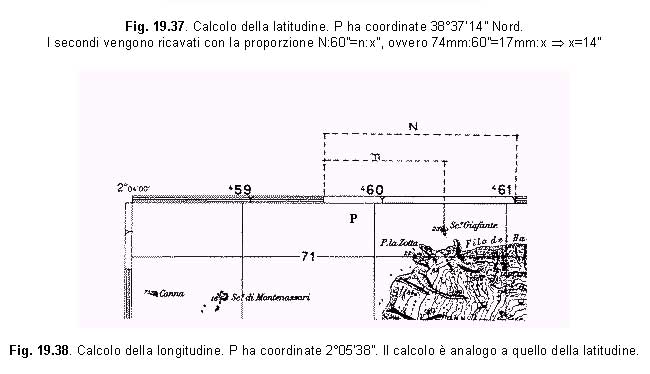
Procedimento inverso Facendo la differenza tra il valore della latitudine del punto e quella del margine inferiore della carta si ottiene un valore, espresso in primi e secondi, che dovrà essere aggiunto a quello del margine inferiore della carta; per i (‘) (interi) da aggiungere sarà sufficienteL’ampiezza corrispondente ai secondi dovrà essere calcolata nel seguente modo:
Per quanto riguarda la longitudine il procedimento è analogo, facendo attenzione al meridiano di riferimento (Greenwich o Monte Mario). SEGNI CONVENZIONALI Vengono indicati come segni convenzionali alcuni simboli che hanno
lo scopo di fornire informazioni aggiuntive in riferimento alla presenza
nella porzione di territorio rappresentata di elementi naturali od artificiali
non altrimenti rappresentabili. Si tratta ovviamente di informazioni
relative alla cartografia di base; le carte tematiche hanno legende
specifiche inerenti il tematismo rappresentato, il quale comunque si
“sovrappone” all’informazione “iniziale”
della cartografia di base. GIS I sistemi informativi territoriali (GIS=Geographic Information System) possono essere definiti, in generale, come un insieme di strumenti per la raccolta, l’organizzazione, il reperimento a piacere, la trasformazione e la visualizzazione di dati spaziali del mondo reale per il raggiungimento di un particolare set di scopi. La descrizione di un sistema informativo territoriale sopra citata, mette in luce due aspetti significativi ad esso legati: - ci sono tante definizioni di GIS quante sono le discipline interessate all’uso di sistemi informativi territoriali (geografia, pianificazione territoriale, ingegneria, architettura del paesaggio, scienze ambientali…) - un GIS consiste in un insieme di strumenti che vengono utilizzati dagli operatori che li utilizzano per migliorare i loro standard lavorativi; nel caso specifico per rendere più efficiente ed efficace il trattamento di informazioni cartografiche e di dati alfanumerici ad esse associati. I GIS contengono informazioni cartografiche digitali delle quali è possibile visualizzare e/o stampare una parte per produrre una particolare cartografia. Una “carta” è quindi uno dei prodotti del GIS così come, ad esempio, un report di stampa è uno dei prodotti di un sistema informativo. Il database dell’informazione cartografica digitale viene creato a partire da vari tipi di cartografia “di base” disponibile in formati e scale quanto mai vari. I dati alfanumerici (attributi) sono informazioni descrittive, organizzate sotto forma di database, riguardanti una qualsiasi caratteristica (feature) che può essere collocata su una carta. Normalmente le feature sono oggetti che hanno una loro realtà fisica (come ad esempio un edificio o una litologia), in altri casi si tratta di entità che, pur non essendo fisicamente visibili, possono comunque essere collocate nella realtà di interesse (ad esempio l’uso del suolo associato ad una certa area). Un caso ancora diverso è quello in cui gli attributi non sono riferiti ad una feature nell’accezione ora definita, ma riguardano particolari “situazioni” che accadono in una certa area (come ad esempio un turno elettorale o un evento sismico). In tutti i casi, comunque, i dati alfanumerici riguardano “oggetti” che, in qualche modo, hanno una collocazione spaziale nell’area in esame (e quindi che possono essere posizionati su una carta). A ciascuno dei dati sopra descritti, indipendentemente dalla loro natura, viene associato un riferimento spaziale (ad esempio un indirizzo, un numero identificativo di un quartiere, un contatore…) a sua volta collegato ad un insieme di coordinate definite in un particolare sistema di riferimento (georeferenziazione [13] ) e registrato su una carta digitale continua della porzione di territorio considerata. Il reperimento, la manipolazione e la visualizzazione dei dati geografici e cartografici sono resi possibili dalla definizione delle relazioni topologiche esistenti tra tutti i punti, linee ed aree contenuti nell’informazione cartografica.
Tecnologie per la cartografia automatizzata Comprendono le componenti hardware e software per la creazione, il mantenimento e la visualizzazione delle informazioni cartografiche digitali. Tipiche componenti hardware sono rappresentate da: - supporti magnetici di memorizzazione (dischi e nastri) - work station grafiche, rappresentate da un insieme di dispositivi per inserire, manipolare editare e visualizzare i dati cartografici. Un esempio di work station grafica è il tavolo di digitalizzazione, che consente di convertire cartografie disponibili su supporto cartaceo in cartografie in forma digitale utilizzabili dai calcolatori (digitalizzazione) - plotter (a penne o elettrostatici), che producono copie cartacee della cartografia digitale - scanner ottici, che digitalizzano automaticamente la cartografia disponibile su supporto cartaceo [14] . Le componenti software associate alle tecnologie per la cartografia automatizzata sono essenzialmente rappresentate dai programmi CAD (Computer Aided Design), contenenti, oltre agli usuali strumenti di disegno, specifiche funzioni utili per la cartografia (trasformazione di coordinate, zoom, calcolo di aree o lunghezze…).
DBMS Nei GIS aiutano a gestire ed integrare i dati raccolti da varie fonti e/o operatori con le caratteristiche rilevate e posizionate nell’area in esame. Un sistema informativo territoriale non fa riferimento ad un unico database per tutte le sue applicazioni, ma esistono più database, relativi ai diversi aspetti analizzati, che possono essere eventualmente collegati tra loro. Il DBMS è particolarmente utile e funzionale per la gestione della parte alfanumerica dei dati contenuti in un GIS (attributi) piuttosto che per quella riguardante i dati cartografici. Ciò dipende sia dal fatto che non esiste uno standard riconosciuto per la gestione di questo tipo di dati, sia dal fatto che i dati cartografici sono più interrelati che i dati alfanumerici, a causa, fondamentalmente, delle relazioni topologiche tra gli oggetti rappresentati nella cartografia (se ad esempio un poligono che rappresenta un’area occupata da una certa litologia viene modificato, anche le relazioni delle aree circostanti con l’area modificata e con le altre intorno dovranno essere modificate: gli attributi geometrici di tutte le aree cambiano). La gestione dei dati spaziali è perciò più complicata rispetto a quella delle tabelle degli attributi alfanumerici; le coordinate ed i dati topologici, fondamentali in un GIS, non appartengono al tradizionale ambiente “tabellare” dei DBMS. Informazione associata ai record territoriali Gli attributi riguardanti una qualsiasi entità territoriale (una particella catastale, un edificio…) possono essere analizzati e manipolati infinite volte con scarso significato se il risultato che si ottiene non viene messo in relazione con la sua collocazione fisica sulla superficie terrestre, cioè se non viene collocato su una carta. Prima dell’avvento delle tecnologie GIS, per l’elaborazione di dati correlati ad una certa collocazione spaziale venivano utilizzati i tradizionali sistemi informativi che producevano report in forma tabellare. Questi report avevano un senso quando venivano utilizzati con una carta di riferimento; spesso gli attributi elencati e riassunti nei report tabulari venivano manualmente trasferiti sulle carte per ulteriori esami ed analisi. Ora che la tecnologia GIS contiene l’informazione cartografica in forma digitale, tuttavia, gli attributi alfanumerici ed i dati cartografici possono essere elaborati insieme come un prodotto singolo con intervento manuale limitato. Per elaborare le informazioni cartografiche insieme ai dati correlati ad una certa collocazione spaziale occorre partire da una base di record territoriali accurata e significativa (una mappa catastale ha un uso limitato se non è messa in relazione con le altre particelle, con la rete stradale…). Non è sufficiente avere accurate informazioni cartografiche, le carte devono esse stesse essere messe in relazione l’una con l’altra e con la loro collocazione fisica sulla superficie terrestre. Inoltre, gli oggetti che la carta rappresenta (intersezioni, particelle, strade…) devono essere identificati sia come dato cartografico sia come attributo alfanumerico, così da correlare il dato alla localizzazione dell’oggetto (ha scarso significato sapere il nome di un proprietario di una particella se la particella stessa non è identificata, quello che si ha è soltanto un nome!). Record territoriali accurati e significativi consentono ad un GIS di correlare i dati alfanumerici ai dati cartografici e di localizzare questa informazione nella sua reale posizione fisica sulla superficie terrestre. I riferimenti utilizzati in un sistema informativo territoriale includono un sistema di coordinate per visualizzare i dati cartografici sotto forma di carta e degli identificatori spaziali per elaborare e visualizzare gli attributi alfanumerici delle feature sulla carta. Questo è un concetto importante nei sistemi informativi territoriali: - memorizzare dati cartografici come un’immagine visiva di una mappa senza collocarli in un sistema di coordinate continuo, impedisce l’uso di quei dati in un contesto territoriale più generalizzato (in questo caso la mappa ha lo stesso uso limitato che può avere la mappa di un atlante “cartaceo”) - memorizzare solamente i dati alfanumerici che descrivono le feature rappresentate non consente di collocare tali dati su una carta (in questo modo i dati possono essere utilizzati solo per stampare liste o report riassuntivi). Le coordinate, i dati cartografici e gli identificatori spaziali formano la base per l’uso dei sistemi informativi territoriali. Alcuni di questi riferimenti sono comuni a tutte le analisi territoriali (ad esempio le strade) mentre altri sono specifici del contesto considerato (ad esempio le specie vegetali presenti in un’area). I riferimenti che sono comuni costituiscono la cosiddetta cartografia di base, in quanto gli altri riferimenti geografici specifici sono basati sulle coordinate, sulle informazioni cartografiche e sugli identificatori spaziali di questi riferimenti comuni. Pur con alcune variazioni, tutte le cartografie di base hanno tre riferimenti generali: - sistema di coordinate, che correla l’informazione cartografica con la superficie terrestre (esempi: UTM, Gauss-Boaga…) - dati cartografici, che rappresentano il livello informativo della cartografia di base (esempi: mappe catastali, ..) - identificatori spaziali, che identificano in maniera univoca feature del territorio rappresentato (segmenti stradali, numero dellle particelle catastali…) Struttura topologica dei dati (topologia) Il computer non “vede” i dati cartografici come un essere umano può vedere una carta. Se consideriamo una carta che riporta delle intersezioni, il computer non può vedere, ad esempio, quali strade sono comuni a tali intersezioni, mentre per noi è immediato constatarlo. La percezione delle “relazioni spaziali” (destra, sinistra, vicino a…) viene appresa presto dagli esseri umani e da quel momento viene applicata sempre implicitamente consentendo, ad esempio, di guardare ad una carta e sapere come e dove gli oggetti che essa rappresenta sono in relazione con gli altri. Il computer, invece, ha bisogno che queste relazioni spaziali siano definite esplicitamente in modi che esso possa comprenderle. Senza la definizione esplicita di come le feature sono in relazione reciproca, non è possibile elaborare i dati geograficamente. Ad esempio, un sistema per la cartografia automatica può riprodurre una carta e, in qualche modo, manipolare una forma (shape) su questa carta. Ma come fa a sapere se questa forma è un poligono (=singola entità geometrica) oppure solo un insieme di linee che si intersecano? Come fa a sapere che una lunga strada è il confine di 3 quartieri? Lo sa definendo queste relazioni esplicitamente. Se la forma è definita come un poligono, allora il computer riconosce il suo confine (boundary) e può, su questa base, realizzare delle analisi (come ad esempio calcolare l’area o campire il poligono all’interno). Se invece la forma è solo un insieme di linee che si intersecano, allora l’area della shape non può essere calcolata né campita. Per poter utilizzare delle funzioni associate ai poligoni, quindi, l’utente deve prima identificarne i confini. Questo, però, rende il sistema difficile da usare; per rendere più efficiente il lavoro è bene definire le relazioni topologiche (come ad esempio i confini dei poligoni, le linee connesse ad una rete…) all’inizio del processo di sviluppo del progetto GIS. Le relazioni sono spesso definite al sistema sotto forma di tabelle. Il computer può “vedere” i valori in queste tabelle per “capire” le relazioni spaziali che gli esseri umani possono vedere sulla carta. La regola da seguire, quindi, per realizzare un GIS è la seguente: affinché il sistema realizzi analisi spaziali usando i dati cartografici, è necessario che tutto ciò che su una carta risulta significativo debba essere esplicitamente definito come un punto, una linea o un poligono [15].Vedere questi oggetti (punti, linee e poligoni) su una carta implicitamente è facile. Rappresentarli per un GIS richiede una definizione esplicita in termini di topologia, identificata da oggetti zero, uni o bidimensionali (con quelli dimensionalmente minori usati per definire quelli dimensionalmente maggiori).
L’analisi spaziale dei dati consente di rielaborare ed estrarre dei sottoinsiemi informativi sulla base dei dati disponibili opportunamente strutturati. In altre parole, l’analisi spaziale consente di associare i vari livelli informativi in modo tale da studiare e rappresentare fenomeni ai quali essi partecipano. Perciò, l’analisi di gruppi di fenomeni (ad es. studio del rischio idrogeologico di un bacino, fatti criminosi di una quartiere…) implicano la determinazione di modelli che indicano avvenimenti non casuali e che perciò necessitano di indagini su altre relazioni per comprendere le motivazioni del raggruppamento di tali fenomeni. Le elaborazioni spaziali, d’altro canto, implicano la manipolazione dei dati dal p.d.v. topologico (sovrapponendo contorni di zone su contorni di aree particolari – es. particelle catastali - determinando la strada più corta tra un incendio e una stazione dei pompieri…) per creare nuova informazione dalle relazioni tra i dati e le strutture topologiche ad essi correlate. In ogni caso, l’analisi spaziale inizia con un problema da risolvere o una domanda a cui rispondere e poi continua con l’esame della cartografia e degli attributi che sono disponibili sulla base di vari metodi statistici, matematici, geometrici e cartografici, che possono essere globalmente indicati come strumenti di analisi spaziali. Gli strumenti di analisi spaziale in un GIS sono dei programmi che reperiscono, manipolano e visualizzano le informazioni geograficamente. Essi, normalmente, prevedono un accesso al database descrittivo per elaborare gli attributi unitamente ai calcoli matematici necessari all’elaborazione del database cartografico dal p.d.v. geometrico (coordinate, distanze ed angoli) tramite l’utilizzo delle relazioni topologiche di punti, linee e poligoni. Molte funzioni geometriche, come la digitalizzazione e l’aggiornamento, la conversione di scala…sono caratteristiche dei sistemi cartografici automatici e non possono essere considerati come strumenti di analisi spaziale. Allo stesso modo, l’elaborazione di dati non grafici, come ad esempio l’inserimento, l’aggiornamento, la ricerca dati…sono normalmente funzioni dei DBMS e quindi non sono tipici del GIS. E’ la manipolazione spaziale dei dati cartografici insieme agli attributi che fa del GIS uno strumento unico (in tal senso). Sebbene le manipolazioni spaziali dei dati possano essere usate per molte analisi diverse, esse iniziano tutte con due domande fondamentali: 1) dov’è (un oggetto)? 2) che cosa c’è (in un posto)? La risposta alla prima domanda, cercando la localizzazione di un attributo su una carta, è semplice senza il computer, se l’attributo in questione è rappresentato sulla carta. A tutti è capitato di guardare una carta per localizzare una particolare entità fisica (una scuola, un parco…). Questo è possibile perché molte carte hanno stampate queste entità e la loro descrizione insieme all’informazione cartografica. Ma quando i dati non sono visualizzati sulla carta, non è possibile identificare tali entità visivamente e determinare la loro posizione. Un GIS, tuttavia, può trovare questi attributi in un database e successivamente correlarli alle caratteristiche cartografiche sulla carta. Una volta che questi attributi sono stati trovati e correlati alla geografia, allora i valori descrittivi degli attributi ed i dati cartografici possono essere manipolati dai programmi di analisi spaziali del GIS per identificare altre relazioni. La risposta alla seconda domanda, cioè la ricerca degli attributi associati ad un’entità collocata in una certa posizione (punto, linea o poligono), è più difficile da dare guardando la carta, dal momento che essa non riporta tutte le informazioni su ogni possibile entità di interesse visualizzata su di essa. Come minimo, per rispondere a questa domanda, occorrerebbe visualizzare molte carte diverse per la stessa area geografica, ciascuna con i suoi record specifici (strade, corsi d’acqua…). Un GIS, tuttavia, può avere vari database con differenti tipi di informazioni, tutte collegate agli stessi riferimenti geografici, cosicché per ogni entità in ogni punto, su una linea o in un poligono è disponibile un insieme di informazioni per compiere l’analisi spaziale. La capacità di compiere analisi spaziali di un GIS permette quindi di rispondere alle due domande di base precedentemente indicate, ed inoltre consente un’interazione tra l’analista ed i dati per investigare le relazioni che riguardano l’argomento o il problema di interesse. Le capacità di analisi possono essere raggruppate in accordo con i tipi di entità associati con le tre unità topologiche fondamentali: punti, linee e poligoni. Analisi dei dati associati a punti - Query spaziali: funzione che consente di trovare e visualizzare gli attributi relativi ad una feature particolare contenuta su una carta (non si tratta di un’analisi spaziale vera e propria, ma è una funzione molto usata) - Geocoding (o geoprocessing): consente di aggiungere, in automatico, identificatori geografici ad un dato insieme di attributi relativo ad una feature in un punto particolare (ad esempio gli attributi comprendenti le indicazioni su indirizzo e numero di particella catastale possono essere completati in automatico con l’aggiunta del nome del comune censuario, provincia…) - Analisi di prossimità: consente la visualizzazione automatica di simboli correlati a feature puntuali che hanno determinati attributi (ad esempio rappresentandoli con dei puntini) e/o l’identificazione di altre feature vicine ad esse. Analisi dei dati associati a linee. - Analisi di rete: la struttura topologica delle linee rende disponibile la possibilità di “seguire” le linee lungo una rete e successivamente di elaborare gli attributi associati con queste linee lungo la rete. Esempi di analisi di rete sono i seguenti: 1) analisi di flusso (associate per esempio alla velocità di flusso dei condotti fognari) 2) analisi di percorso. Il tragitto di un veicolo lungo una rete di strade, come ad esempio un mezzo dei vigili del fuoco diretto verso un incendio, è identificato sulla base dei segmenti stradali (linee) che collegano il punto di partenza (n° identificativo della caserma dei vigili del fuoco) alla destinazione (n° identificativo della zona in cui c’è l’incendio). Quando sono possibili più percorsi, si analizzano gli attributi associati ai segmenti delle linee (tempo di percorrenza, distanza…) per calcolare i totali di ogni percorso e selezionare, sulla base di questi totali, la distanza o il tempo di percorrenza più corti tra i 2 punti (percorso ottimale) Analisi dei dati associati a poligoni - Elaborazione relativa ai poligoni: intesa come funzione che utilizza i limiti dei poligoni per identificare quali punti, linee o altri poligoni elaborare. I contorni del poligono definiscono i limiti delle coordinate dei punti, linee e poligoni da elaborare: ciò che è fuori non viene elaborato, ciò che è dentro si. 1) Funzioni di “punto-in-poligono”: identificano quali punti sono collocati all’interno di un poligono. Gli attributi delle feature rappresentate da questi punti possono essere utilizzati per produrre statistiche, visualizzare simboli su una carta o stampare liste su report tabellari. 2) Funzioni di “riempimento di poligoni”: utilizzano le statistiche calcolate dalle funzioni precedenti (oppure calcolate o ottenute da altre fonti) per campire o colorare l’area entro i limiti del poligono. La campitura o il colore sono determinati dalla grandezza (importanza) del valore della statistica calcolata (normalmente definito da un intervallo di valori). 3) Funzioni di “sovrapposizione (overlay) di poligoni”: utilizzano operatori logici Booleani (AND, OR, NOT…) per creare nuovi poligoni a partire dai limiti di 2 o più poligoni. Le aree entro i nuovi poligoni hanno gli attributi che sono delle combinazioni Booleane dell’insieme originale di poligoni. - Poligonizzazione, intesa come creazione di poligoni dai dati invece di creazione di limiti di poligoni dalla digitalizzazione. Questi poligoni vengono creati sulla base di determinati criteri spaziali definiti dall’utente. 1) Funzioni di aggregazione spaziale: creano dei poligoni sulla base di risultati di clustering spaziale come ad es. quelli mostrati da una carta di densità di punti. 2) Funzioni di buffering: formano un poligono attorno ad una punto, linea o un altro poligono piazzando il suo contorno ad una certa distanza dalla feature. |
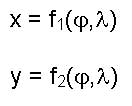
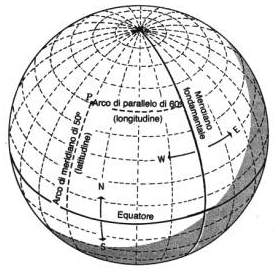



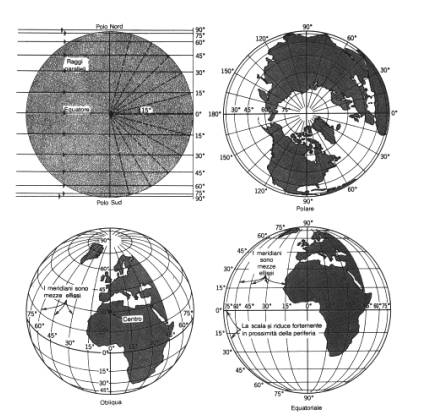 Fig.
19.2
Fig.
19.2